Learn how to use the implemented probability distributions in INOSIM to add stochastic failures or process parameters to your model, and how to set up your custom distribution.
Probability distributions in simulation
One advantage of simulations are the always reproducible and therefore comparable results. That allows us to compare different scenarios, identify and solve bottlenecks, and last but not least, it simplifies the debugging of models. But there are situations in which this reproducibility is not desired. For example, if failure times of equipment should be investigated, certain input parameters of a model are subject to uncertainties, or, if a specific operation should only be executed in a specific fraction of times, randomness must be brought into the simulation.
Using the implemented probability distributions
With INOSIM, this is either possible by using already implemented probability distributions or a random number generator. Using the implemented distributions comes with the advantage that all generated random values are actually pseudorandom. This means they are randomly generated but at the same time reproducible as long as the seed value in the settings of the simulation or the sequence of random numbers is not changed (see Fig. 1). This again makes simulation runs comparable and simplifies the debugging.
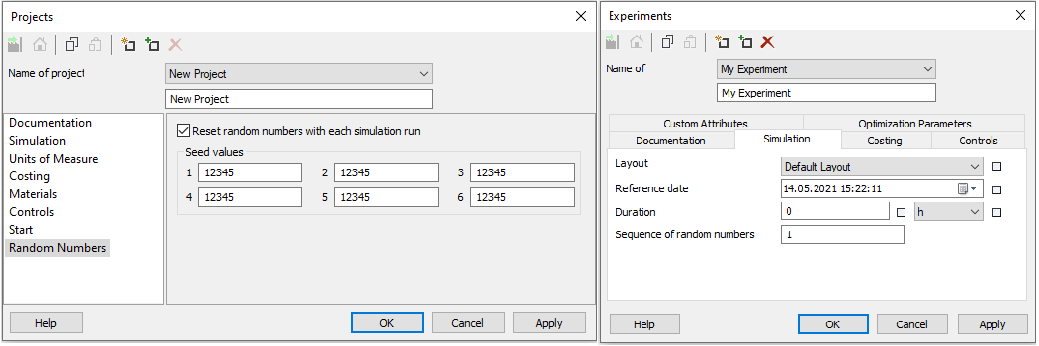
Figure 1: Property window of the project (left) and the experiment (right). Here, the seed values and the sequence of random numbers can be changed.
There are already ten different probability distribution types available in INOSIM. They can either be used directly, for example in the property window of units for failures or maintenance (see Fig. 3) or via VBA. Via VBA, either the distribution itself can be assigned to a property (e.g., the FailureDuration property of a unit) or a sample value of the distribution to an arbitrary variable in INOSIM (see examples below).
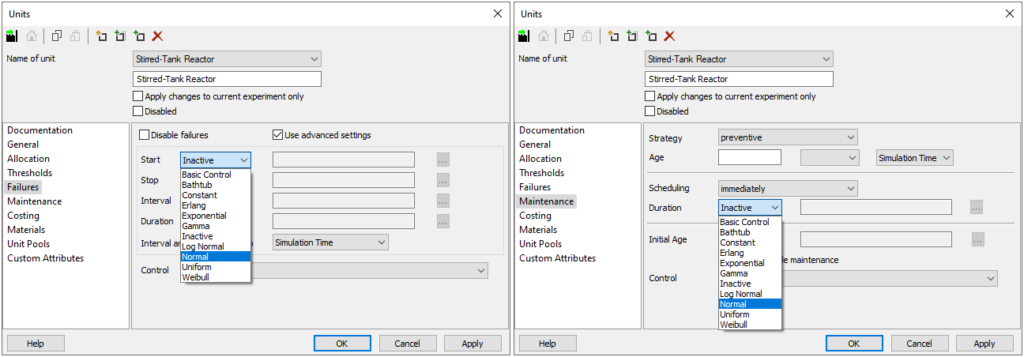
Figure 2: Failures tab (left) and Maintenance tab (right) of the property window of a unit. Here the implemented probability distributions can be chosen to define the intervals and the duration of failures and maintenance.
An example of how an assignment via VBA could look like is shown below. Here, a specific operation should only be executed in 20 % of the times. To achieve this, an alternative branch with a link condition is used and the shown control is assigned to the link condition. In this case a uniform distribution is used.
Sub LinkCondition((cond As OrderLinkCondition)
Dim distr As New Uniform
Dim value As Double
distr.Start = 0 'Lower bound
distr.Stop = 1 'Higher bound
value = distr.Sample 'Uniformly distributed value is saved in variable
if value <= 0.2 Then
cond.value = True 'Operation will be executed
Else
cond.value = False 'Operation won't be executed
End If
End SubAnother example of using a distribution in your simulation is given below. A normal distribution is used to define the duration and an exponential distribution to define the interval of failures of a specific unit in the initialization phase of the simulation. Here, instead of a sample value of the chosen distribution the distribution itself is assigned to the FailureDuration or the FailureInterval property.
Private Sub Simulation_Init()
Dim nor As New Normal
nor.Mu = 2 * 3600 '[h]
nor.Sigma = 2 * 3600 * 0.1 '[h]
Set Units("Stirred-Tank Reactor").FailureDuration = nor
Dim expo As New Exponential
expo.Beta = 24 * 3600 '[h]
Set Units("Stirred-Tank Reactor").FailureInterval = expo
End SubDefinition of custom distributions
If the given distribution types are not suitable for your problem, it is possible to create any other custom distribution types out of the given ones. Custom distributions are often used to create discretely or triangularly distributed values. A discrete distribution can easily be generated out of the uniform distribution implemented in INOSIM as shown below. The Round function returns the uniformly generated variable rounded to an integer.
Function discrete_distribution() As Double
Dim distr As New Uniform
distr.Start = 0 'Lower bound
distr.Stop = 10 'Higher bound
discrete_distribution = distr.Sample 'Uniformly distributed value is saved in variable
discrete_distribution = Round(discrete_distribution) 'Uniformly distributed value is rounded to an integer
End FunctionTriangular distribution
The triangular distribution is often used as a simplification of the normal distribution if the sample data is not sufficient to determine a significant mean or standard deviation. It also shows the typical behavior of a higher probability of occurrence the closer the randomly generated value is to the expected value. On the other hand there is no standard deviation needed to describe the distribution (see Fig. 1). One way to create a triangular out of a uniform distribution in INOSIM is the function triangular_distribution shown below. It needs the low and high bound as well as the most probable value as inputs and returns a triangularly distributed value of the type Double.
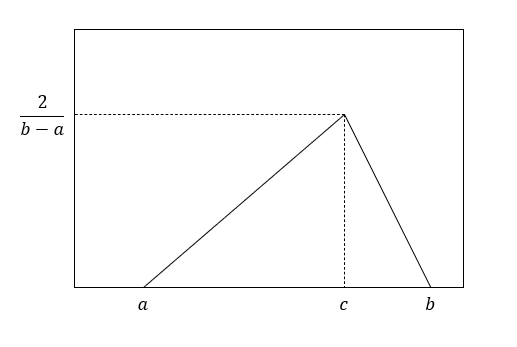
Figure 3: Triangular distribution with the lower bound a, the higher bound b and the mode c
Function triangular_distribution(d_Min As Double,d_Mode As Double, d_Max As Double) As Double
Dim dRand As Double
Dim dc_a As Double
Dim db_a As Double
Dim dc_b As Double
If d_Mode <= d_Min Or d_Max <= d_Mode Then
Console.Error "Mode is not between lower and higher bound."
Exit Function
End If
dc_a = d_Max - d_Min
db_a = d_Mode - d_Min
dc_b = d_Max - d_Mode
Dim dre As New Uniform 'Uniformly distributed value between 0 and 1 is generated
dre.Start = 0
dre.Stop = 1
dRand = dre.Sample
If dRand < db_a / dc_a Then 'Uniformly distributed value is converted to triangulary distributed value
triangular_distribution = d_Min + Sqr(dRand * db_a * dc_a)
Else
triangular_distribution = d_Max - Sqr((1 - dRand) * dc_a * dc_b)
End If
'[see Vose: Risk Analysis, 2nd ed., p. 128]
End FunctionThe function can be called in your simulation as shown below. Here an uncertainty is assigned to the mass flow through a specific unit. This time the triangular distribution is used to describe the uncertainty.
Sub call_triangular_distribution
Dim mass_flow As Double
Dim Mean_flow As Double
Dim min_flow As Double
Dim max_flow As Double
Mean_flow = 100 'Expected value of the triangular distribution
min_flow = 80 'Lower bound
max_flow = 120 'Higher bound
mass_flow = triangular_distribution(min_flow,Mean_flow,max_flow)
End SubBeta distribution
A third example of how a custom distribution can be implemented in INOSIM is shown here with the beta distribution. The beta distribution is a family of continuous probability distributions that can take different shapes depending on the parametrization (see Fig. 2). A beta distributed value can easily be generated out of two gamma distributed values (G. S. Fishman. Monte Carlo – Concepts, Algorithms, and Applications. Springer, New York, 1. Edition, 1996). The gamma distribution is already implemented in INOSIM and therefore a beta distribution can be created with the function Beta_distribution shown below. It needs the two shape parameters α and β as inputs and can be called in the same way as the function for the triangular distribution.
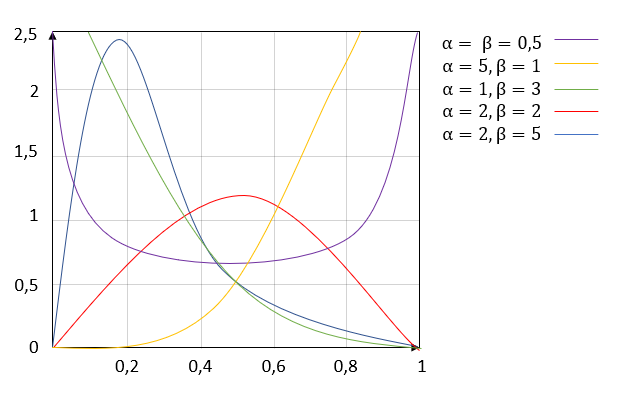
Figure 4: Beta distribution with different shape parameters α and β
Function Beta_distribution(alpha As Double, beta As Double) As Double
Dim X As Double
Dim Y As Double
Dim gam1 As New Gamma 'First gamma distributed value is generated
gam1.Alpha = alpha
gam1.Beta = 1
X = gam1.Sample
Dim gam2 As New Gamma 'Second gamma distributed value is generated
gam2.Alpha = beta
gam2.Beta = 1
Y = gam2.Sample
Beta_distribution = X/(X+Y) 'Gamma distributed values are converted to beta distributed value
End Function- PDF printout of this Tip & Trick
More Questions?
Want to know more about this topic or have another question? Please contact us!
More Tips & Tricks
Event Call Sequence
As an experienced INOSIM user, you are aware that you are working with a discrete-event simulation software. For most events, VBA controls can be called…
Preventing Runtime Errors and Custom Error Handling
This Tip & Trick describes a multitude of methods to prevent and handle runtime errors of your VBA code. You will be introduced to the…
Modeling Fluctuating Resource Demands
In the process industry, it is not unlikely that a resource demand changes over the time of a process operation. Typical examples are cooling jackets…
General Inquiries 
