Hier lernen Sie, wie Sie die eingebauten Wahrscheinlichkeitsverteilungen von INOSIM nutzen, um stochastische Störungen oder Prozessparameter in Ihr Modell zu integrieren, und wie Sie Ihre benutzerdefinierte Verteilung erstellen.
Wahrscheinlichkeitsverteilungen in der Simulation
Ein Vorteil von Simulationen sind die immer reproduzierbaren und daher vergleichbaren Ergebnisse. Das erlaubt es uns, unterschiedliche Szenarien zu vergleichen, Engpässe zu erkennen und zu beheben und nicht zuletzt vereinfacht es das Debuggen von Modellen. Doch es gibt Situationen, in denen diese Reproduzierbarkeit nicht erwünscht ist. Wenn beispielsweise Ausfallzeiten von Anlagen untersucht werden sollen, bestimmte Eingangsparameter eines Modells mit Unsicherheiten behaftet sind oder wenn eine bestimmte Operation nur in einem bestimmten Anteil an Fällen ausgeführt werden soll, muss Zufälligkeit in die Simulation eingebracht werden.
Anwendung der eingebauten Wahrscheinlichkeitsverteilungen
Mit INOSIM ist dies durch die Verwendung bereits implementierter Wahrscheinlichkeitsverteilungen oder eines Zufallszahlengenerators möglich. Die Verwendung der implementierten Verteilungen hat den Vorteil, dass alle generierten Zufallswerte tatsächlich pseudozufällig sind. Sie sind also zufällig generiert, aber gleichzeitig reproduzierbar, solange die Seedwerte in den Einstellungen der Simulation oder die Sequenz der Zufallszahlen nicht verändert werden (siehe Abb. 1). Dies macht Simulationsläufe wiederum vergleichbar und vereinfacht das Debuggen.
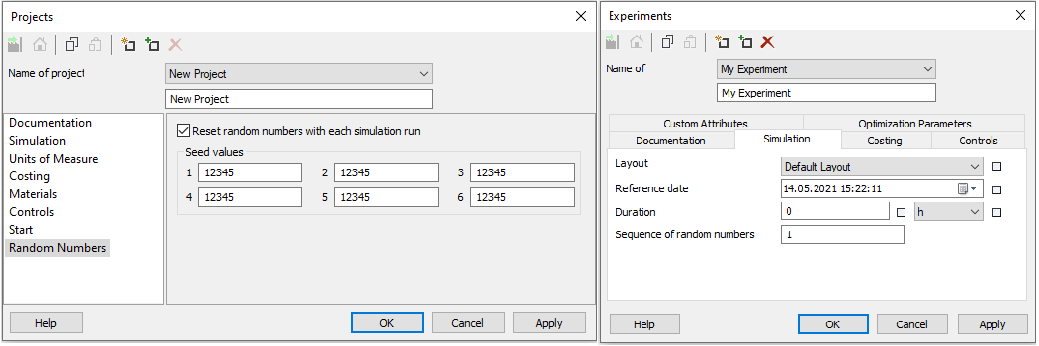
Abbildung 1: Eigenschaftsfenster für Projekt (links) und Experiment (rechts). Hier können die Seedwerte und die Sequenz der Zufallszahlen geändert werden.
In INOSIM stehen bereits zehn verschiedene Wahrscheinlichkeitsverteilungstypen zur Verfügung. Sie können entweder direkt, z. B. im Eigenschaftsfenster von Teilanlagen für Störungen oder Wartung (siehe Abb. 3), oder via VBA gesetzt werden. Über VBA kann entweder die Verteilung selbst einer Eigenschaft zugeordnet werden (z. B. die FailureDuration-Eigenschaft einer Teilanlage) oder ein Samplewert der Verteilung zu einer beliebigen Variable in INOSIM (siehe Beispiele unten).
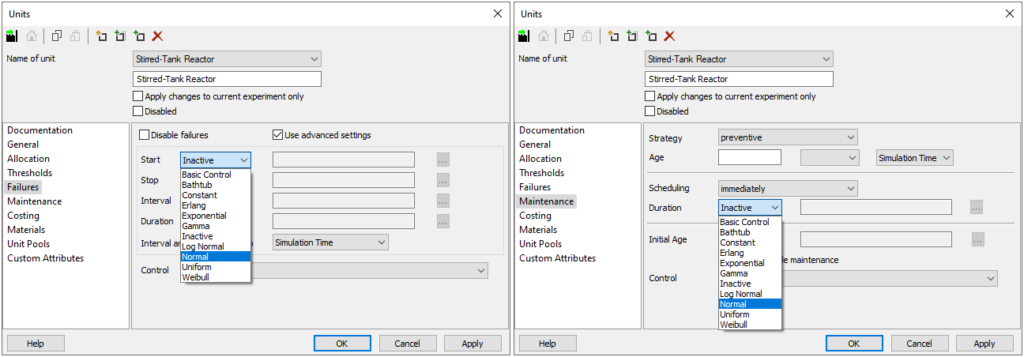
Abbildung 2: Reiter Failures (links) und Maintenance (rechts) des Eigenschaftenfensters einer Teilanlage. Hier können die eingebauten Wahrscheinlichkeitsverteilungen ausgewählt werden, um Intervalle und Dauer von Störungen und Wartung zu definieren.
Ein Beispiel, wie eine Zuweisung über VBA aussehen kann, ist unten gezeigt. Hier sollte eine bestimmte Operation nur in 20% der Fälle ausgeführt werden. Dazu wird eine Alternativverzweigung mit einer Verknüpfungsbedingung verwendet und die gezeigte Steuerung der Verknüpfungsbedingung zugeordnet. In diesem Fall wird eine Gleichverteilung verwendet.
Sub LinkCondition((cond As OrderLinkCondition)
Dim distr As New Uniform
Dim value As Double
distr.Start = 0 'Unterer Schwellenwert
distr.Stop = 1 'Oberer Schwellenwert
value = distr.Sample 'Gleichverteilter Wert wird in der Variable gespeichert
If value <= 0.2 Then
cond = True 'Operation wird ausgeführt
Else
cond = False 'Operation wird nicht ausgeführt
End If
End SubEin weiteres Beispiel für die Verwendung einer Verteilung in Ihrer Simulation finden Sie im Folgenden. Eine Normalverteilung wird verwendet, um die Dauer, und eine Exponentialverteilung, um das Intervall der Störungen einer bestimmten Teilanlage in der Initialisierungsphase der Simulation zu definieren. Hier wird anstelle eines Samplewerts der gewählten Verteilung die Verteilung selbst der FailureDuration– oder der FailureInterval-Eigenschaft zugewiesen.
Private Sub Simulation_Init()
Dim nor As New Normal
nor.Mu = 2 * 3600 '[h]
nor.Sigma = 2 * 3600 * 0.1 '[h]
Set Units("Stirred-Tank Reactor").FailureDuration = nor
Dim expo As New Exponential
expo.Beta = 24 * 3600 '[h]
Set Units("Stirred-Tank Reactor").FailureInterval = expo
End SubDefinition benutzerdefinierter Verteilungen
Wenn die gegebenen Verteilungstypen nicht für Ihr Problem geeignet sind, ist es möglich, aus ihnen weitere, benutzerdefinierte Verteilungstypen zu erstellen. Benutzerdefinierte Verteilungen werden häufig verwendet, um diskret- oder dreiecksverteilte Werte zu erstellen. Aus der in INOSIM implementierten Gleichverteilung kann, wie unten gezeigt, leicht eine diskrete Verteilung generiert werden. Die Round-Funktion gibt die gleichverteilte Variable auf eine ganze Zahl gerundet zurück.
Function discrete_distribution() As Double
Dim distr As New Uniform
distr.Start = 0 'Unterer Grenzwert
distr.Stop = 10 'Oberer Grenzwert
discrete_distribution = distr.Sample 'Gleichförmig verteilter Wert wird in der Variable gespeichert
discrete_distribution = Round(discrete_distribution) 'Gleichförmig verteilter Wert wird nach Integer aufgerundet
End FunctionTrianguläre Verteilung
Die Dreiecksverteilung wird häufig als Vereinfachung der Normalverteilung verwendet, wenn die Stichprobenanzahl nicht ausreicht, um einen signifikanten Mittelwert oder eine Standardabweichung zu bestimmen. Es zeigt sich ebenfalls das typische Verhalten einer höheren Eintrittswahrscheinlichkeit, je näher der zufällig generierte Wert am Erwartungswert liegt und gleichzeitig ist für die Beschreibung der Verteilung keine Standardabweichung erforderlich (siehe Abb. 1). Eine Möglichkeit, aus einer Gleichverteilung in INOSIM eine Dreiecksverteilung zu erzeugen, ist die unten gezeigte Funktion triangular_distribution. Sie benötigt die unteren und oberen Grenzwerte sowie den am häufigsten auftretenden Wert als Input und gibt einen dreiecksverteilten Wert vom Typ Double zurück.
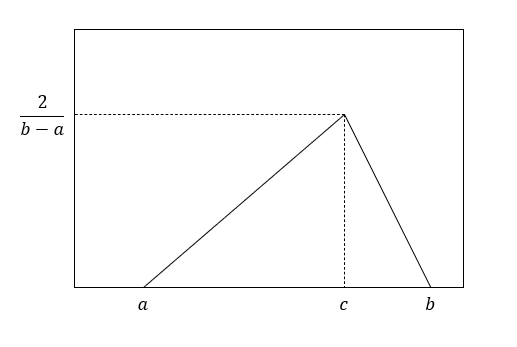
Abbildung 3: Dreiecksverteilung mit unterem Grenzwert a, oberem Grenzwert b und Modalwert c
Function triangular_distribution(d_Min As Double,d_Mode As Double, d_Max As Double) As Double
Dim dRand As Double
Dim dc_a As Double
Dim db_a As Double
Dim dc_b As Double
If d_Mode <= d_Min Or d_Max <= d_Mode Then
Console.Error "Modalwert liegt nicht zwischen unterem und oberen Grenzwert."
Exit Function
End If
dc_a = d_Max - d_Min
db_a = d_Mode - d_Min
dc_b = d_Max - d_Mode
Dim dre As New Uniform 'Gleichverteilter Wert zwischen 0 und 1 wird generiert
dre.Start = 0
dre.Stop = 1
dRand = dre.Sample
If dRand < db_a / dc_a Then 'Gleichverteilter Wert wird zu dreiecksverteiltem Wert konvertiert
triangular_distribution = d_Min + Sqr(dRand * db_a * dc_a)
Else
triangular_distribution = d_Max - Sqr((1 - dRand) * dc_a * dc_b)
End If
'[see Vose: Risk Analysis, 2nd ed., p. 128]
End FunctionDie Funktion kann in Ihrer Simulation wie unten gezeigt aufgerufen werden. Hier wird dem Materialfluss durch eine bestimmte Teilanlage eine Unsicherheit zugeordnet. Dieses Mal wird die Dreiecksverteilung verwendet, um die Unsicherheit zu beschreiben.
Sub call_triangular_distribution
Dim mass_flow As Double
Dim Mean_flow As Double
Dim min_flow As Double
Dim max_flow As Double
Mean_flow = 100 'Erwarteter Wert der triangulären Verteilung
min_flow = 80 'Unterer Grenzwert
max_flow = 120 'Oberer Grenzwert
mass_flow = triangular_distribution(min_flow,Mean_flow,max_flow)
End SubBeta-Verteilung
Ein drittes Beispiel, wie eine benutzerdefinierte Verteilung in INOSIM implementiert werden kann, wird hier mit der Beta-Verteilung gezeigt. Die Beta-Verteilung ist eine Familie von kontinuierlichen Wahrscheinlichkeitsverteilungen, die je nach Parametrisierung unterschiedliche Formen annehmen können (siehe Abb. 2). Ein betaverteilter Wert lässt sich leicht aus zwei gammaverteilten Werten generieren (G. S. Fishman. Monte Carlo – Concepts, Algorithms, and Applications. Springer-Verlag, New York, 1. Edition, 1996.). Die Gamma-Verteilung ist bereits in INOSIM implementiert und daher kann mit der unten gezeigten Funktion Beta_distribution eine Beta-Verteilung erzeugt werden. Sie benötigt die beiden Formparameter α und β als Inputs und kann auf die gleiche Weise aufgerufen werden wie die Funktion für die Dreiecksverteilung.
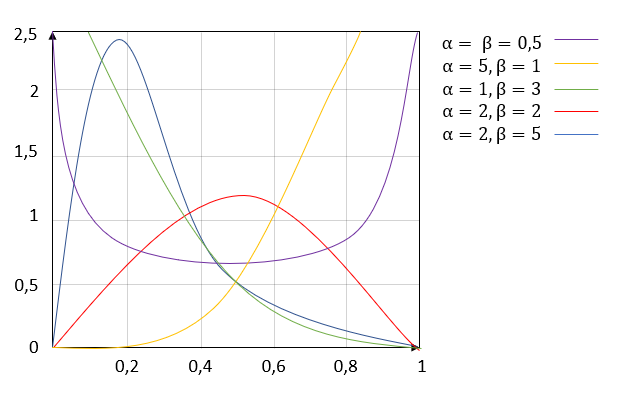
Abbildung 4: Beta-Verteilung mit verschiedenen Formparametern α und β
Function Beta_distribution(alpha As Double, beta As Double) As Double
Dim X As Double
Dim Y As Double
Dim gam1 As New Gamma 'Erster gammaverteilter Wert wird erzeugt
gam1.Alpha = alpha
gam1.Beta = 1
X = gam1.Sample
Dim gam2 As New Gamma 'Zweiter gammaverteilter Wert wird erzeugt
gam2.Alpha = beta
gam2.Beta = 1
Y = gam2.Sample
Beta_distribution = X/(X+Y) 'Gammaverteilte Werte werden zu betaverteilten Werten konvertiert
End Function- PDF-Ausdruck zu diesem Tipp & Trick
Fragen?
Möchten Sie mehr über dieses Thema erfahren oder haben weitere Fragen? Bitte kontaktieren Sie uns.
Mehr Tipps & Tricks
INOSIM Fernsteuerung über die COM-Schnittstelle
Wussten Sie, dass INOSIM mit jedem Programm ferngesteuert werden kann, das Signale über die COM-Schnittstelle senden kann? Hier erfahren Sie, wie dieses Feature verwendet werden…
Oft werden INOSIM-Modelle von mehreren Personen gewartet. Eine Herausforderung besteht dann darin, allen Beteiligten die aktuellste Version zur Verfügung zu stellen und sie konsistent zu…
Modellierung von veränderlichen Ressourcenbedarfen
In der Prozessindustrie ist es nicht ungewöhnlich, dass sich der Bedarf an Ressourcen über eine Prozessoperation ändert. Typische Beispiele hierfür sind Kühlmäntel von Reaktoren, in…





